In probability theory and statistics, Bayes’ theorem (alternatively Bayes’ law or Bayes’ rule; recently Bayes–Price theorem[1]:44, 45, 46 and 67), named after the Reverend Thomas Bayes, describes the probability of an event, based on prior knowledge of conditions that might be related to the event.[2] For example, if the risk of developing health problems is known to increase with age, Bayes’ theorem allows the risk to an individual of a known age to be assessed more accurately (by conditioning it on their age) than simply assuming that the individual is typical of the population as a whole.
摘自维基百科
One of the many applications of Bayes’ theorem is Bayesian inference, a particular approach to statistical inference. When applied, the probabilities involved in the theorem may have different probability interpretations. With Bayesian probability interpretation, the theorem expresses how a degree of belief, expressed as a probability, should rationally change to account for the availability of related evidence. Bayesian inference is fundamental to Bayesian statistics.
上文的翻译请各位童鞋自行解决,简单总一下贝叶斯定律是一种计算概率的公式,这个概率的计算考虑了与随机事件相关的因素;一句话就是它所阐述了后验概率的获得方法。
朴素贝叶斯模型发源于古典数学理论,有着坚实的数学基础,以及稳定的分类效率;对大数量训练和查询时具有较高的速度,即使使用超大规模的训练集,针对每个项目通常也只会有相对较少的特征数,并且对项目的训练和分类也仅仅是特征概率的数学运算而已;对小规模的数据表现很好,能个处理多分类任务,适合增量式训练(即可以实时的对新增的样本进行训练);对缺失数据不太敏感,算法也比较简单,常用于文本分类;朴素贝叶斯对结果解释容易理解。
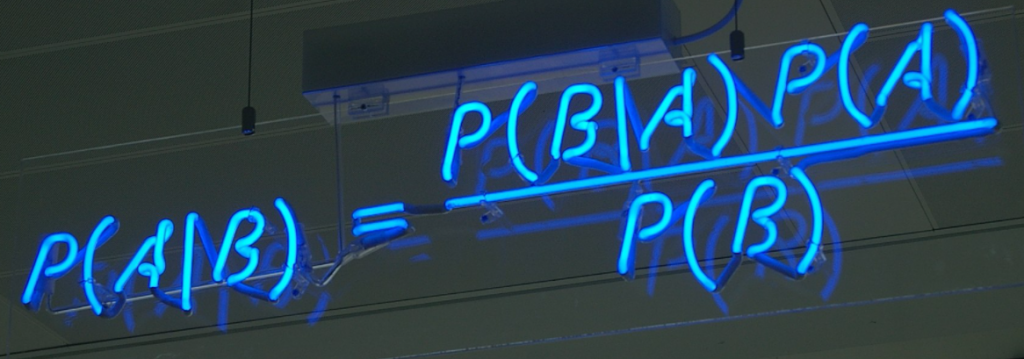
预备知识点一:
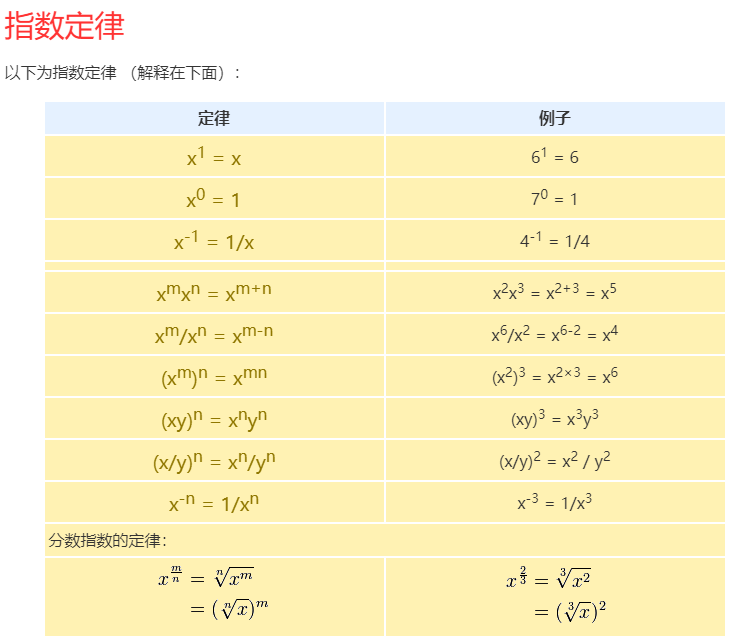

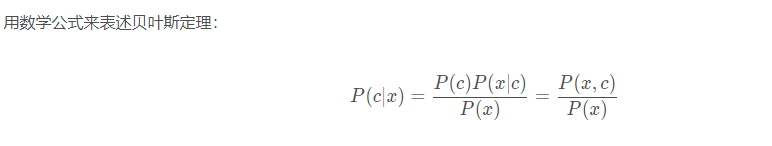
c表示的是随机事件发生的一种情况。x表示的就是证据(evidence)/状况(condition),泛指与随机事件相关的因素。
- P(c|x):在x的条件下,随机事件出现c情况的概率。(后验概率)
- P( c ):(不考虑相关因素)随机事件出现c情况的概率。(先验概率)
- P(x|c):在已知事件出现c情况的条件下,条件x出现的概率。(后验概率)
- P(x):x出现的概率。(先验概率)
一般情况下,我们在实际的问题当中,我们想获得的核心结果其实也就是P(c|x),举个现实的栗子?场景来对应P(c|x)的话就可以是这样的:
X 代表一个话,如“我喜欢这部手机”,而 C 表示的是这句话的情感,如“积极”,”消极”–> 那么P(c|x) 表示的就是 “我喜欢这部手机” 是“积极/消极” 的概率有多大。
而从计算上来说,我们需要同时知道P( c ),P(x|c)和P(x)才能算出目标值P(c|x)。“而P(x)对于是c无关的,而且作为共同的分母,在我们计算c的各种取值的可能性时并不会对各结果的相对大小产生影响,因此可以忽略”。(这段话是什么意思呢?用下边的例子说明)
比如c可取值c 1 , c 2 , c 3,并假设已知
p(c1)=o, p(c2)=p, p(c3)=q,P(x|c1)=a, P(x|c2)=b, P(x|c3)=c, p(x)=m
那么最后计算p(c|x)时,分别会得到结果
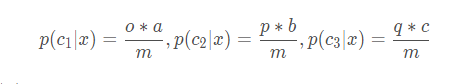
由于p(c_1|x)+p(c_2|x)+p(c_3|x)的和一定为1,固我们可以得到o a + p b + q c = m oa+pb+qc=moa+pb+qc=m,而即使m的值预先不知道也没关系,因为oa,pb,qc的值都是可以计算出来的,m自然也就得到了。所以略掉了P(x)后,最后难点也就落在了计算P(x|c)与P( c )上,而这两个概率分布是必须要通过我们手上有的数据集来进行估计的。
p(c)的获得其实也较为简单:假设我们有了一个数据集D,计算D中c的各个情况出现的频率即可。比如计算P(c1),直接用c1情况出现次数在所有情况中所占的比例值即可–>例如“喜欢”这个词在”积极”情感词的情况下出现了5词,而积极词总量是10000, 那么P(c1)=5/10000(这里用到了大数定律:当训练集包含充足的独立同分布样本时,P(c)可通过各类样本出现的频率来进行估计。)
但是,获得p(x|c)就略显困难,因为x往往包含多个相关因素(是一个多种因素构成的向量),即它可能有多个需要考虑的属性值:x=(x1,x2,x3,…,xn);任一xi都代表了所有相关因素中的其中一个。当x是一个向量时,我们若要计算P(x|c),实际上就是要计算P ( x 1 , x 2 , x 3 , . . . , x n ∣ c )这个理论上也是可以利用我们的数据集D来进行估计的,但是现实情况是,n的值往往非常大(属性非常多),而我们的数据集往往不能保证我们的样本包含了属性值的所有可能组合(假设每个属性都是二值属性,那么就有2n种属性组合)。那么很多p(x|c)我们估计得到的值就是0。然而这些样本很可能仅仅是我们的数据集中没包含到,即“未被观测到”,但不代表它们现实中“出现概率为0”。于是这就给我们计算出真实合理的目标p(c|x)值造成了障碍。
这个时候朴素贝叶斯的“朴素”就要来发挥作用了,我们为了能够获得合理的p(x|c)的值,采用了“很不科学”的属性条件独立性假设。

由于朴素贝叶斯分类器在这种naive的假设下仍能在实际问题中取得比较好的效果,因此这个假设的不合理性在某些情况下也就可以不用特别计较了。




当然以上都是最简单的入门讲解,朴素贝叶斯也有很多的变种,有兴趣的同学可以去自行搜索相关的资料,笔者也会在后期文章中慢慢补充
- Tree augmented Bayesian Classifier(TAN)
- Bayesian Network augmented Bayesian Classifier(BAN)
- Semi-Naive Bayesian Classifiers(SNBC)
- Multidimensional Bayesian Network Classifiers(MBC)
- Bayesian chain classifiers(BCC)
