机器学习-拉普拉斯平滑（Laplacian smoothing）

零概率和拉普拉斯修正

拉普拉斯平滑(Laplacian smoothing) 是为了解决零概率的问题。拉普拉斯是一个人名，他是法国数学家，并且最早提出用 加1 的方法来估计没有出现过的现象的概率。

零概率问题：在计算事件的概率时，如果某个事件在观察样本库（训练集）中没有出现过，会导致该事件的概率结果是0。这是不合理的，不能因为一个事件没有观察到，就被认为该事件一定不可能发生（即该事件的概率为0）。至于可能出现零概率问题的情况在贝叶斯定理实现是容易出现。

理论假设：假定训练样本很大时，每个分量x的计数加1造成的估计概率变化可以忽略不计，但可以方便有效的避免零概率问题。

举一个例子?来说明一下，如下图，有很多的“0”值，如何把零值影响规避掉呢？

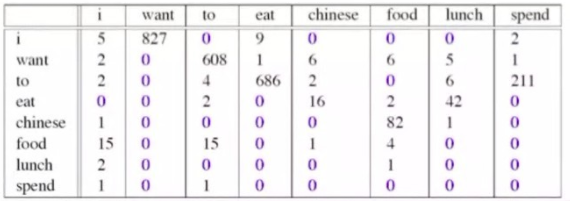
previous : P(wi | wi-1) = c(wi-1, wi) / c(wi)
using smoothing: P(wi | wi-1) = ( c(wi-1, wi) + 1 ) / (c(wi-1) + V)
Then we can ensure that the p will not be zero. Now we can estimate this mothed.
We can use the Reconsitituted formula: c(wi-1, wi) = P(wi | wi-1) * c(wi-1) = ( c(wi-1, wi) + 1 ) / (c(wi-1) + V) * c(wi-1).

总结：分子加一，分母加V，V代表类别数目。

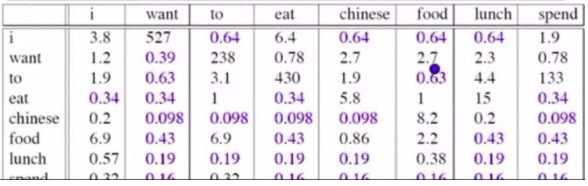
再进一步总结就如下：

场景举栗子：

假设在文本分类中，有3个类：C1、C2、C3。
在指定的训练样本中，某个词语K1，在各个类中观测计数分别为0，990，10。
则对应K1的概率为0，0.99，0.01。

显然C1类中概率为0，不符合实际。

于是对这三个量使用拉普拉斯平滑的计算方法如下：
　　1/1003 = 0.001，991/1003=0.988，11/1003=0.011
　　
在实际的使用中也经常使用加 λ（0≤λ≤1）来代替简单加1。如果对N个计数都加上λ，这时分母也要记得加上N*λ