数据结构-二叉树基础 二叉树前序、中序、后续遍历的理解

树是数据结构中较为基础但是又很重要的知识点。文章将着重介绍一般二叉树、完全二叉树、满二叉树等基本概念做入门介绍，以及对树的遍历和存储做概念性的讲解，希望为那些对数据结构有求知欲的童鞋提供有效的帮助。我们会从树的定义可以看出，树的定义使用了递归的方式。递归在树的学习过程中起着重要作用。

一个普通的树

1、树的定义

树（Tree）是n（n>=0)个结点的有限集。n=0时称为空树。在任意一颗非空树中：
1）有且仅有一个特定的称为根（Root）的结点；
2）当n>1时，其余结点可分为m(m>0)个互不相交的有限集T1、T2、……、Tn，其中每一个集合本身又是一棵树，并且称为根的子树。

此外，树的定义还需要强调以下两点：
1）n>0时根结点是唯一的，不可能存在多个根结点，数据结构中的树只能有一个根结点。
2）m>0时，子树的个数没有限制，但它们一定是互不相交的。

2、树的度、层级、节点关系、深度

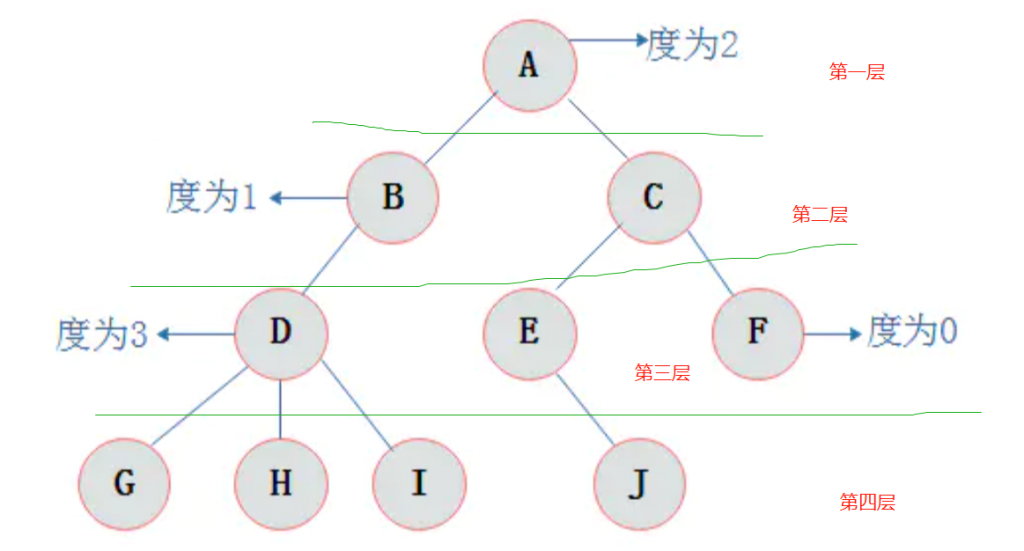
  • 结点的度：结点拥有的子树数目称为结点的度。
  • 结点子树的根结点为该结点的孩子结点。相应该结点称为孩子结点的双亲结点。同一个双亲结点的孩子结点之间互称兄弟结点。
  • 树中结点的最大层次数称为树的深度或高度。
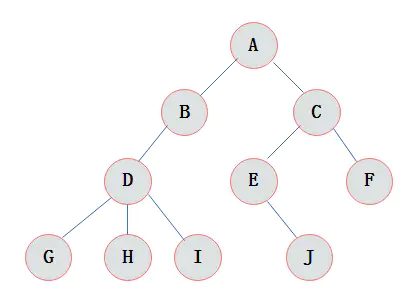
  • 从根开始定义起，根为第一层，根的孩子为第二层，以此类推。如下图中

1.A为B的双亲结点，B为A的孩子结点。

2.结点B与结点C互为兄弟结点。

3.树的深度为4

树的度和层

3、二叉树的定义

二叉树是n(n>=0)个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。

斜树：所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树。

斜树

4、二叉树的性质和特点

性质啊

1）在二叉树的第i层上最多有2i-1 个节点 。（i>=1）
2）二叉树中如果深度为k,那么最多有2k-1个节点。(k>=1）
3）n0=n2+1 n0表示度数为0的节点数，n2表示度数为2的节点数。
4）在完全二叉树中，具有n个节点的完全二叉树的深度为[log2n]+1，其中[log2n]是向下取整。
5）若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号，则对完全二叉树中任意一个编号为 i 的结点有如下特性：

(1) 若 i=1，则该结点是二叉树的根，无双亲, 否则，编号为 [i/2] 的结点为其双亲结点;
(2) 若 2i>n，则该结点无左孩子， 否则，编号为 2i 的结点为其左孩子结点；
(3) 若 2i+1>n，则该结点无右孩子结点， 否则，编号为2i+1 的结点为其右孩子结点。

特点呀

1）每个结点最多有两颗子树，所以二叉树中不存在度大于2的结点。
2）左子树和右子树是有顺序的，次序不能任意颠倒。
3）即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。5、

5、满二叉树、完全二叉树

满二叉树：在一棵二叉树中。如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。
满二叉树的特点有：
1）叶子只能出现在最下一层。出现在其它层就不可能达成平衡。
2）非叶子结点的度一定是2。
3）在同样深度的二叉树中，满二叉树的结点个数最多，叶子数最多。

完全二叉树：对一颗具有n个结点的二叉树按层编号，如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树。

特点：
1）叶子结点只能出现在最下层和次下层。
2）最下层的叶子结点集中在树的左部。
3）倒数第二层若存在叶子结点，一定在右部连续位置。
4）如果结点度为1，则该结点只有左孩子，即没有右子树。
5）同样结点数目的二叉树，完全二叉树深度最小。
注：满二叉树一定是完全二叉树，但反过来不一定成立。

左边满二叉树，右边完全二叉树

6、二叉树遍历

二叉树的遍历是指从二叉树的根结点出发，按照某种次序依次访问二叉树中的所有结点，使得每个结点被访问一次，且仅被访问一次。

先序、中序、后序：遍历过程中经过结点的路线一样，只是访问各结点的时机不同。

1.先序遍历

① 访问根结点；② 先序遍历其左子树； ③ 先序遍历其右子树。

通俗的说就是从二叉树的根结点出发，当第一次到达结点时就输出结点数据，按照先向左在向右的方向访问。如下图，先序遍历的结果是：

A（B D F E ）（C G H I）=> A B D F E C G H I

先序遍历
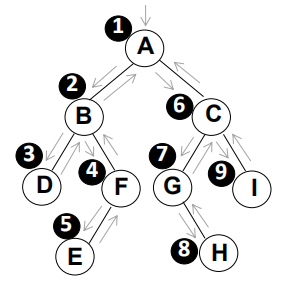
从根结点出发，则第一次到达结点A，故输出A;
继续向左访问，第一次访问结点B，故输出B；
按照同样规则，输出D；
当到达叶子结点D，返回到B，此时已经是第二次到达B，故不在输出B，进而向B右子树访问，B右子树不为空，则访问至F，第一次到达F，则输出F；继续向F的左节点E访问，第一次到达E,则输出E;
E为叶子结点，则返回到F，F左子树已经访问完毕,其没有右子树，则返回到B，进而到B左右子树子树访问完毕，则返回到A, A为根节点，它有右子树，则访问C,第一次到达C，故输出C；
向C左子树，故输出G；
按照同样的访问规则，继续输出H、I；
2.中序遍历

① 中序遍历其左子树； ② 访问根结点； ③ 中序遍历其右子树。

就是从二叉树的根结点出发，当第二次到达结点时就输出结点数据，按照先向左在向右的方向访问。如下图，中序遍历的结果是：

（D B E F） A （G H C I）=> D B E F A G H C I

中序遍历
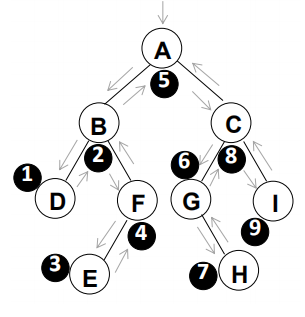
从根结点出发，则第一次到达结点A，不输出A，继续向左访问，第一次访问结点B，不输出B；继续到达D，此时第一次到达D,不输出D,继续访问D的左子树，D的左子树为空，则返回到D，此时第二次到达D,输出D;
D的右子树是空，向上返回到B,第二次到达B,则输出B；
B有右子树，访问F,第一次到达不输出，向F的左子树访问E,第一次访问不输出，但是E没有左子树，访问点返回到E，则输出E;
从叶子节点E返回到F，第二次访问，输出F;F向上返回到B,第三次到达不输出；
B向上返回到A,第二次到达输出A;
A的左子树结束了，开始右子树，按照同样的逻辑输出G、H、C、I；
3.后序遍历

① 后序遍历其左子树； ② 后序遍历其右子树； ③ 访问根结点。

就是从二叉树的根结点出发，当第三次到达结点时就输出结点数据，按照先向左在向右的方向访问。如下图，后序遍历的结果是：

（D E F B ）（ H G I C） A => D E F B H G I C A

后序遍历
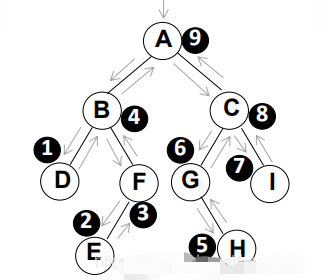
从根结点出发，则第一次到达结点A，不输出A，继续向左访问，第一次访问结点B，不输出B；继续到达D，第一次到达不输出，尝试访问D的左子树，没有则返回到D,第二次访问依旧不输出，尝试访问D的右子树，没有则返回到D，第三次访问，则输出D;
D返回到B,第二次访问不输出；
访问B的右子树F,第一次访问不输出，到达E,叶子节点E输出；
E向上放回到F,第二层访问不输出，尝试F的右子树，没有则返回到F,第三次访问，则输出F;
F向上放回到B,第三次访问，输出B；
B向上放回到根节点A,第二次访问，不输出A;
A左子树访问完开始右子树,先到C，G,都是第一次访问不输出；
G向左尝试没有左子树，则开始尝试右子树，存在右子树H;
H假装尝试左右子树都没有，因为H是叶子节点，这个尝试过程发生了第三次范文H,则输出H;
继续访问后续节点依次输出G、I、C、A

发表回复