我们在之前数据结构-二叉树基础的篇幅中已经对二叉树(binary tree)的基本性质、特点做了入门介绍,不再做过多的介绍。本篇旨在通过最简单的python代码来模拟实现二叉树的先序遍历、中序遍历、后序遍历。
二叉树是有限个元素的集合,该集合或者为空、或者有一个称为根节点(root)的元素及两个互不相交的、分别被称为左子树和右子树的二叉树组成。
二叉树的基本介绍
1、特点知识回顾
- 二叉树的每个结点至多只有二棵子树(不存在度大于2的结点),二叉树的子树有左右之分,次序不能颠倒。
- 二叉树的第i层至多有2^{i-1}个结点
- 深度为k的二叉树至多有2^k-1个结点;
- 对任何一棵二叉树T,如果其终端结点数为N0,度为2的结点数为N2,则N0=N2+1
2、上代码
# 定义基本二叉树结构
class Node:
def __init__(self,value=None,left=None,right=None):
self.value=value
self.left=left #左子树
self.right=right #右子树
def preTraverse(root):
'''
前序遍历
'''
if root==None:
return
print(root.value)
preTraverse(root.left)
preTraverse(root.right)
def midTraverse(root):
'''
中序遍历
'''
if root==None:
return
midTraverse(root.left)
print(root.value)
midTraverse(root.right)
def afterTraverse(root):
'''
后序遍历
'''
if root==None:
return
afterTraverse(root.left)
afterTraverse(root.right)
print(root.value)
3、验证
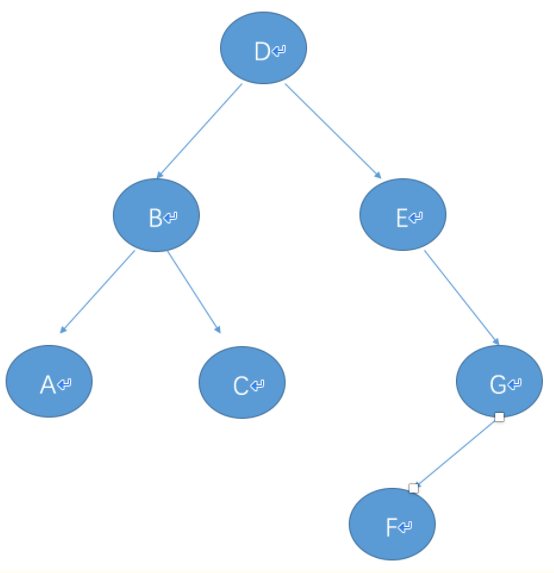
root=Node('D',Node('B',Node('A'),Node('C')),Node('E',right=Node('G',Node('F'))))
print('前序遍历:')
preTraverse(root)
print('\n')
print('中序遍历:')
midTraverse(root)
print('\n')
print('后序遍历:')
afterTraverse(root)
print('\n')
前序遍历:
D
B
A
C
E
G
F
中序遍历:
A
B
C
D
E
F
G
后序遍历:
A
C
B
F
G
E
D
